If you’re involved in digital marketing or product development in some way, you already know just how vital A/B testing is for making data-driven decisions.
At the heart of A/B testing is statistical power. This is actually a critical component in determining the test’s effectiveness in detecting differences between variants.
This article discusses statistical power in A/B testing in detail, giving you complete insights into what it is, the factors affecting it, and the steps involved in measuring it.
From pre-test analysis, including estimating sample size and determining effect size, to post-test analysis, interpreting results, and making informed decisions, this article covers each phase of A/B testing with detailed insights and practical approaches.
What Is Statistical Power in A/B Testing?
Statistical power in A/B testing is a crucial concept. It determines the effectiveness of the test in detecting an actual effect if there is one.
In simpler terms, it’s the test’s ability to detect a change or improvement when one version is better or different.
What makes statistical power so crucial in A/B testing?
High statistical power means a higher chance of detecting a true positive (a real difference between groups A and B). Low power increases the risk of a Type II error (failing to detect a real effect), leading to potentially incorrect conclusions about the effectiveness of the variables being tested.
Here are some factors that might influence the statistical power:
- Effect Size: Larger effect sizes (differences between groups) are easier to detect, increasing power.
- Sample Size: Larger sample sizes generally increase power, more accurately representing the tested populations.
- Significance Level (Alpha): Setting a lower significance level (e.g., 0.01 instead of 0.05) makes the test more stringent but can decrease power.
- Variability in Data: Less variability within each group leads to higher power, as detecting a difference between groups is easier.
Measuring Statistical Power in A/B Testing
Pre-Test Analysis
1. Estimating Required Sample Size
The sample size is the number of observations or data points (such as users or transactions) needed in each group of the A/B test to detect a difference if one exists reliably.
If your sample size is too small, it may lead to unreliable results. On the other hand, if your sample size is too large, it may waste resources.
Before calculating the sample size, you need to define the expected effect size – the difference you expect to see between the two groups. You can base this on industry standards, previous tests, or business objectives.
The next step is to select a Significance Level (Alpha). Typically set at 0.05, this is the probability of rejecting the null hypothesis when it is true (Type I error). A lower alpha reduces the chance of false positives but requires a larger sample size.’
After that, choose a Power Level (1 – Beta). Commonly set at 0.80 or 0.90, this is the probability of correctly rejecting the null hypothesis when the alternative hypothesis is true. Higher power requires a larger sample size.
Finally, estimate the variability or standard deviation in your data. More variability means you’ll need a larger sample size to detect an effect.
To conduct the final calculations, you can use statistical formulas incorporating the effect size, significance level, desired power, and variability.
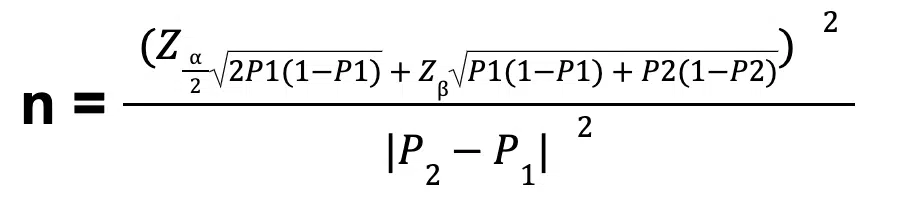
Statistical formula (Source)
From the formula above, here are all the variables stated:

Statistical formula variables (Source)
Alternatively, you can use various online calculators and statistical software tools available to simplify this calculation of sample sizes by inputting the desired effect size, alpha, power, and variability.
2. Determining Effect Size
Effect size is the magnitude of the difference between groups that the test is designed to detect. It’s a measure of how impactful the change is.
Knowing the effect size helps in understanding the practical significance of the test results, thereby helping you calculate the sample size and set realistic expectations.
Here are some ways to help you determine your effect size:
- Mean difference: A common way to calculate the effect size for continuous data is Cohen’s d, which is the difference between two means divided by the standard deviation.
- Proportional difference for rates and proportions: For binary outcomes (like conversion rate), the effect size can be the difference in proportions or a ratio.
- Using pilot studies: Conducting a small-scale pilot test can also provide preliminary data to estimate a more accurate effect size.
3. Choosing an Appropriate Significance Level
The significance level, often denoted as alpha (α), determines the threshold for statistical significance and plays a vital role in interpreting test results.
Simply put, the significance level is the probability of rejecting the null hypothesis when it is actually true. In other words, it’s the risk of a Type I error – falsely identifying an effect without one.
The most common significance levels in A/B testing are 0.05 (5%) and 0.01 (1%). A 5% level means there is a 5% chance of concluding that a difference exists when there is no actual difference.
In most cases, the tester chooses the alpha level before the test begins, and it’s not adjusted based on the data. This fixed approach prevents bias in the interpretation of results.
Conducting the A/B Test
Now that you’ve done the pre-test analysis, it’s finally time to conduct the A/B test. Here’s how to go about the process:
1. Implementing the Test Design
This phase involves putting into action the plan developed during the pre-test analysis – making sure you execute the test in a way that yields reliable and legitimate results.
Before you start, confirm the elements you plan to test (e.g., webpage design, email campaign content). Ensure these elements are well-defined and the changes between the control (A) and variant (B) are clear and measurable.
After that, determine how to select and assign the participants or data points to the control or test group. This is typically done through randomization to ensure that the two groups are comparable and that the results are not biased by external factors.
For the uninitiated, randomization helps in controlling for confounding variables and ensures that any observed effect can be attributed to the changes being tested.
After that, follow this step-by-step process to implement the test design:
- Sample Size and Power Considerations: Implement the sample size decided upon in the pre-test analysis. Remember that the sample size must meet the requirements to achieve the desired statistical power.
- Setting Up the Test Environment: Ensure that the testing environment is controlled and consistent. For online testing, this might involve setting up the necessary software tools or platforms to display the variations to different users.
- Monitoring for Test Integrity: Throughout the test, monitor for any issues that might affect its integrity, such as technical problems or unexpected external factors.
- Data Collection: Collect data rigorously and ensure you collect all the relevant information. This includes not only the primary metric(s) of interest but also any auxiliary data that might help in interpreting the results (more on this in the next section).
While implementing the test design, make sure you avoid sources of bias, including selection bias, measurement bias, or experimenter bias. Ensure that the methods of data collection and analysis are objective and consistent.
2. Data Collection Methods
After you implement the test design, the next step is to collect the data meticulously to ensure the reliability and accuracy of the results.
The best way to go about it is by using software tools and technologies suited for A/B testing. For websites or apps, this may include analytics platforms like FigPii or custom-built tools.
Here are the data collection methods you can use:
- Random Sampling: Randomly assign participants or data points to either the control group or the experimental group to avoid selection bias and ensure that the groups are comparable.
- User Tracking: Don’t forget to track user interactions with the product through cookies, session IDs, and more.
- Time-Stamping: Record the time when data is collected. This will help you determine how results may vary over different periods and controlling for time-based variables.
- Automated Data Collection: Automation helps in collecting large volumes of data with minimal error. This can include automated event tracking on websites or apps.
- Qualitative Data Collection: In addition to quantitative data, qualitative data, like user feedback, will give you insights into certain user behaviors or preferences.
Post-Test Analysis
1. Calculating Observed Power
The observed power is the probability that the test correctly rejected the null hypothesis (which states that there is no difference between the two groups) given the observed effect size, sample size, and significance level.
It’s a post-hoc analysis that tells you how likely your test was to detect the effect you observed.
Calculating observed power helps in interpreting the results of the A/B test. If a test has low observed power, any non-significant findings (failure to reject the null hypothesis) might be due to the test not being sensitive enough rather than the absence of a real effect.
So, how will you test the observed power? Here are some tips:
- Using Statistical Software: You can use statistical software like R, Python, or specialized tools like G*Power to calculate the observed power. These tools have built-in functions to calculate power based on the test’s parameters.
- Input Parameters: To calculate observed power, you need the observed effect size from your test, the sample size of each group, and the alpha level (significance level) you used.
- Statistical Methods: The calculation often involves determining the non-centrality parameter based on the observed effect size and then using this parameter to find the power. For example, in a two-sample t-test, the non-centrality parameter is calculated, and then the cumulative distribution function is used to find the power.
2. Interpreting the Results
This process involves looking beyond the mere statistical significance to understand the practical implications of the results.
Begin by determining if the results are statistically significant. You can do it by comparing the p-value from your statistical test to the pre-set alpha level (e.g., 0.05). A p-value lower than the alpha level indicates statistical significance.
That said, statistical significance alone won’t give you an idea of practical significance.
Make sure you evaluate the effect size, which refers to the difference between the two groups. For example, a small but statistically significant effect might not be practically relevant.
And as we’ve already discussed, review the observed power of the test. A high observed power strengthens confidence in the results, especially if the test results are not significant.
3. Making Decisions Based on Test Outcomes
Once you gain insights into the test, it’s time to turn those insights into actionable steps.
This process involves interpreting the test results in the context of business or research objectives and then making informed decisions about the implementation of changes based on these results.
Before making decisions, thoroughly interpret the test outcomes, considering statistical significance, effect size, and observed power. Understand not just whether the results are statistically significant but also if they are practically significant for your specific context.
Another important factor is assessing how the results align with business goals or research objectives. For instance, even a slight increase in conversion rate might be significant for a large ecommerce business.
Consider the following when making decisions based on your test outcomes:
- Positive Results: If the test shows a positive outcome (for example, the variant performs significantly better than the control), decide if the improvement is worth the cost and effort of implementation. Consider scalability and long-term implications.
- Negative or Neutral Results: For negative or non-significant results, determine whether it’s best to abandon the changes, make modifications, or conduct further testing. Sometimes, non-significant results can provide valuable insights for future tests.
- Risk Assessment: Assess the risks of implementing the changes based on the test outcomes. This includes considering the potential impact on user experience, brand perception, and potential expenditures.
Based on the above outcomes, plan for a full-scale rollout if you finally decide to implement the changes. Make sure to inform all stakeholders and make necessary adjustments for a smooth transition.
If the results remain uncertain, don’t hesitate to conduct further tests or iterations to gather more data and insights.
Regardless of the decision, document the test process, results, and your decisions. This will help you refer to the document in the future or build a knowledge base for future assessments.
Over to You!
Making sense of statistical power is key to successful A/B testing. It’s like making sure you have a strong enough magnifying glass to see the details of your experiment clearly.
Each step is important, from deciding how many people to include in your test (sample size) to figuring out what size of change you’re looking for (effect size). After running the test, you can’t overlook determining whether your test was good enough to find real differences.
Finally, you carefully look at what the numbers are telling you and decide what to do next.
In simple terms, this guide helps you make sure that your A/B tests are set up right, run smoothly, and the results are used in the best way to improve your product or strategy.



